Keywords for Modules DSCF and RIDFT

$denconv real

Convergency criterion for the root mean square of the density matrix. If you want to calculate an analytical MP2 gradient (program mpgrad) real should be 1.d-7 or less.

$dft options

Listing of all possible sub-keywords for $dft (cross-references are given).

The user normally has to choose only the functional and the grid size, see below. All other parameters have proven defaults.

functional name

Specification of the functional, default is BP86, printed as functional b-p. For all possible--and useful--functionals, please refer to page and for definition of the functionals the section 6.2 on page .

Example (default input):

$dft
   functional b-p

gridsize integer or minteger

Specification of the spherical grid (see section 15.2.5 on page ). Default is gridsize m3.

Example:

$dft
   gridsize m3

gridtype integer

    --not recommended for use--
Specification of the mapping of the radial grid.

Possible values for gridtype are 1,…, 6, but gridtype 4 to 6 is only for the use with functional lhf (see page ). For the definition of gridtype 1 - 3, please refer to Eq. (16), (17) and, (19) in Ref. [131].

Example (default value):

$dft
   gridtype 3

debug integer

Flag for debugging. debug 0 means no debug output (default), debug 1 means some output, debug 2 means a lot more output. Be careful!

nkk integer

Specification of the sharpness of the partition function as proposed by Becke [132], default is nkk 3. The usage of nkk makes sense only in the range 1≤ nkk ≤6.

Example:

$dft
   nkk 3

$\parbox{2.7cm}{\texttt{ntheta} \textit{integer}\\ \texttt{nphi} \textit{integer}}$

    --not recommended for use--

Only for user-specified Lobatto grids, i.e. gridsize 9, ntheta specifies the number of θ points and nphi specifies the number of φ points. For the fixed Lobatto grid, i.e. gridtype 8, the default value is ntheta 25 and nphi 48.

When gridsize 9 is given, you have to specify both, ntheta and nphi (see below), otherwise the program will crash. The restriction for user-defined Lobatto grids is the number of grid points, which must not exceed 2000 grid points.

Example:

$dft
  gridsize 9
  ntheta 30
  nphi 60

old_RbCs_xi

Original grids had not been carefully optimized for all atoms individually. This has now been done, which let to changes of ξ for Rb and Cs only resulting in minor improvements. If you have ongoing projects, which have been started with the old grids, you should continue using them with the keyword old_RbCs_xi.

Example:

$dft
   old_RbCs_xi

radsize integer

Specifies the number of radial grid points. Default values depend on type of atom and grid (see keyword gridsize). The formula for the radial gridsize is given as,

ioffrad is atom-dependent, the more shells of electrons, the larger ioffrad:

elements ioffrad elements ioffrad

for H-He 20 for K-Kr 40

for Li-Ne 25 for Rb-Xe 45

for Na-Ar 30 for Cs-Lw 50

The radial grid size increases further for finer grids:

gridsize 1 2 3 4 5 6 7 8 9

radsize 1 2 3 6 8 10 14 9 3

If you want to converge results with respect to radial grid size, increase radsize in steps of 5, which is convenient (see equation above).

diffuse integer

Serves to increase quadrature grids; this is recommended in case of very diffuse wavefunctions. With the keyword diffuse grids are modified by changing the linear scaling factor ξ of radial grid points and the radial gridsize:

radsize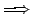 $\Longrightarrow$ radsize + incr
ξ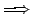 $\Longrightarrow$ ξ * scal

diffuse integer 1 2 3 4 5 6

incr 1 2 3 4 5 6

scal 1.5 2.0 2.8 4.0 5.0 6.0

For information about the linear scaling parameter ξ, see Eq. (16)-(19) and Table 1 in Ref. [131].

In addition, the reduction of spherical grid points near nuclei is supressed, i.e. fullshell on is set (see page ).

Note: the keyword radsize integer overrules the setting of incr; for more information, see p. .

Recommendation: For diffuse cases use gridsize m4 (or larger) in combination with diffuse 2 and check the number of electrons; for more difficult cases use diffuse 4. In case of doubt, verify the calculation with a larger grid, i.e. gridsize 7.

The test suite example $TURBODIR/TURBOTEST/dscf/short/H3PO4.DSCF.DIFFUSE provides an example of usage; this also gives reasonable values for damping and orbitalshift to reach convergence in this and similar cases, see $scfdamp and $scforbitalshift (p. and p. ).

Example (Recommendation):

$dft
  gridsize m4
  diffuse 2

$\parbox{3cm}{\texttt{rhostart} \textit{integer}\\ \texttt{rhostop} \textit{integer}}$

    --for developers only--

Radial grid points have a linear scaling parameter ξ, see Eq.(16)-(19) and Table 1 in Ref. [131]. With the following input,

$dft
   rhostart 50
   rhostop 200

one performs a numerical integration for the density and the exchange correlation term for ξ = 0.5,(0.01), 2.0 for given MOs and functional. NOTE: only molecules with a single atom type can be used. The results serve to establish stable, optimal ξ values, see Figure 1 in Ref. [131]. Program stops after this testing.

reference

Usage of the reference grid, which is a very fine grid with very tight thresholds. The default values for the different variables are:

gridsize 7
radsize 14
fullshell 1
dgrenze 16
fgrenze 16
qgrenze 16
fcut 16

Please refer to the corresponding sub-keywords for explanation.

If you want to use the reference grid, you have to skip the keyword gridsize, and type instead reference. Example:

$dft
   functional b-p
   reference

test-integ

Check if the selected grid is accurate enough for the employed basis-set by performing a numerical integration of the norm of all (occupied and virtual) orbitals. Useful for LHF. .

batchsize integer

Grid points are sorted into batches, which are then processed. This increases efficency. This should be changed only by developers. Default is batchsize 100.

fullshell

Standard grids have reduced number of spherical grid points near nuclei. With the keyword fullshell this reduction is suppressed. Reference grid (see keyword reference) always has full spherical grids with 1202 points. Should be used to checked the influence of spherical grid reduction.

Example for the usage of fullshell:

$dft
   functional b-p
   gridsize m4
   fullshell

$\parbox{3cm}{\texttt{symblock1} \textit{real}\\ \texttt{symblock2} \textit{real}}$

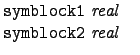
    --for developers only--

Values of real effects efficiency of the quadrature, default is symblock1 0.001 and symblock2 0.001, one can try higher or smaller values.

xparameter integer

    --not recommended for use--
Where xparameter (default) can be: sgrenze (8), fgrenze (10), qgrenze (12), dgrenze (12) and, fcut (14). These parameters control neglect of near zeros of various quantities. With xparameter integer one changes the default. integer larger than defaults will increase the numerical accuracy. Tighter threshold are set automatically with keyword $scfconv (see section 15.2.5 on page ).

weight derivatives

Includes the derivatives of quadrature weights to get more accurate results. Default is that the derivatives of quadrature weights will be not considered, see section 15.2.8 on page .

gridordering

Grid points are ordered into batches of neighbouring points. This increases efficiency, since now zeros can be skipped for entire batches. gridordering is default for serial version, not for the parallel one. You cannot use weight derivatives and gridordering together.

Example for switching off gridordering:

$dft
   gridordering 0

$electrostatic field

Specification of external electrostatic field(s). The specification may take place either by Ex, Ey, Ez or by x, y, z, |E|. See also $fldopt.

Example:

$electrostatic field
       0.1000E-03   0.000       0.000

$fermi tmstrt=<300.0> tmend=<100.0> tmfac=<0.9> hlcrt=<1.0E-01> stop=<1.0E-03> nue=<N>

Requests calculation of occupation numbers at a finite temperature T. For an orbital with the energy $\varepsilon_{{i}}^{}$ the occupation number n_i∈$\left[\vphantom{ 0,1}\right.$0, 1$\left.\vphantom{ 0,1}\right]$ is calculated as

n_i = $${\frac{{1}}{{2}}}$$erfc$$\left(\vphantom{ \frac{\varepsilon _{i}-\mu }{fT}}\right.$$$${\frac{{\varepsilon _{i}-\mu }}{{fT}}}$$$$\left.\vphantom{ \frac{\varepsilon _{i}-\mu }{fT}}\right)$$,

where μ is the Fermi level. The factor f = 4k/$\sqrt{{\pi}}$ is chosen to yield the same slope at the Fermi level as the Fermi distribution.

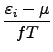
Calculation of the fractional occupation numbers starts when the current HOMO-LUMO gap drops below the value given by hlcrit (default: 0.1). The initial temperature given by tmstrt (default: 300K) is reduced at each SCF cycle by the factor tmfac (default: 1.0) until it reaches the value tmend (default: 300K). Note that the default values lead to occupation numbers calculated at a constant T = 300K. Current occupation numbers are frozen if the energy change drops below the value given by stop (default: 1 ⋅10^-3). This prevents oscillations at the end of the SCF procedure.

Calculation of fractional occupation numbers often requires much higher damping and orbital shifting. Please adjust the values for $scfdamp and $scforbitalshift if you encounter convergence problems.

In UHF runs this option can be used to automatically locate the lowest spin state. In order to obtain integer occupation numbers tmend should be set to relatively low value, e.g. 50K.

Calculation of fractional occupation numbers should be used only for single point calculations. When used during structure optimizations it may lead to energy oscillations.

The optional nue value (number of unpaired electrons) can be used to force a certain multiplicity in case of an unrestricted calculation. nue=0 is for singlet, nue=1 for dublet, etc.

$firstorder

Perform first-order SCF-calculation, i.e. perform only one SCF-iteration with the start MOs (which should be the orthogonalized MOs of two independent subsystems as is explained in detail in Chapter 13).

$fldopt options

Specification of options related with external electrostatic fields. The following options are available:

1st derivative on/off

Calculate numerical 1st derivative of SCF energy with respect to electrostatic field (default: off), increment for numerical differentiation is edelt (see below).

2nd derivative on/off

Calculate numerical 2nd derivative of SCF energy with respect to electrostatic field (default: off), increment for numerical differentiation is edelt.

edelt= real

Increment for numerical differentiation (default: 0.005).

fields on/off

Calculate SCF energy for non-zero external electrostatic
fields defined in $electrostatic field.

geofield on/off

Calculate SCF energy for one external field definition and dump disturbed MOs onto $scfmo. This enables to evaluate properties or perform geometry optimizations in the presence of an external field.

Caution: don't use the RI approximation for all these calculations since this will lead to non-negligible errors!!

$incore integer

By using this option the two-electron integrals are kept in RAM; integer specifies how many megabytes should be allocated. If the integrals exceed the RAM allocated the program reverts to the standard mode. Supports all methods which process two-electron integrals, i.e. SCF and DFT (including hybrid functionals); RHF and UHF.

The following condition must be met:

$scfdenapproxl 1

and rhfshells 1 or 2. It is advisable to set $thize as small as possible (e.g. $thize 0.1d-08) and to remove the keyword $scfdump.

Note: this keyword does not work for parallel runs.

$mo-diagram only nirreps=integer

If this keyword is set the energies and symmetry labels of all occupied MOs will be dumped to this data group. This may be helpful to draw mo-diagrams. If only has been set only the start MOs are dumped and the program quits.

nirreps will hold the total number of displayed orbitals after the successful run.

$moprint

If this keyword is present all occupied orbitals are dumped to standard output. Be careful about this option as it can create huge output files in case of many basis functions.

$mo output format format

If this line is present, the dscf program is forced to output the MOs using the new FORTRAN format format regardless of the format-option in data group $scfmo. Otherwise the input format will be used.

Example: $mo output format(3(2x,d15.8))

$natural orbitals

This data group will be written after an UHF calculation (together with $natural orbital occupation) and contains the natural space orbitals (same syntax as $scfmo).

$natural orbital occupation

This data group will be written after an UHF calculation (together with $natural orbitals) and contains the occupation of natural orbitals (syntax as any data group related with orbital occupation information, e.g. $closed shells), e.g.

 a       1-5                     (     2.00000000000000 )
 a       6                       (     1.99949836999366 )
 a       7                       (     1.99687490286069 )
 a       8                       (     1.00000000000000 )
 a       9                       (      .00312509713931 )
 a       10                      (      .00050163000634 )

$point_charges

Specification of position and magnitude of point charges to be included in the Hamiltonian. Each point charge is defined in the format

<x> <y> <z> <q>

with , , being the coordinates and its charge,e.g.

$point_charges thr=<real> self-energy list 
   2. 2. 2. 5.
   5. 0. 0. 2.5

In addition the following optional arguments may be given:

thr

distance threshold for discarding redundant point charges, default value 10^-6.

selfenergy

if given, the selfenergy of the point charge array will will be included in the energy and the gradient

list

print all point charges in the output (default is to print the point charges only if less than 100 charges given)

$prediag

concerns the first SCF iteration cycle if start MOs from an EHT guess are used.

The SCF iteration procedure requires control mechanisms to ensure (fast) convergence, in TURBOMOLE these are based on orbital energies ε_i of the preceeding iteration used for level shifting and damping (besides DIIS, see below). This feature cannot be used in the first iteration if EHT MOs are employed as start, since ε_i are not available. The keyword $prediag provides ' ε_i of the zeroth iteration' by diagonalization of occ-occ and virt-virt part of the first Fock matrix, to allow for level shifting etc.. See $scfdiis below.

$restart dscf twoint

Try a dscf restart. The program will read the data group $restartd (which must exist, also $scfmo has to exist!) and continue the calculation at the point where it ended before. If the additional option twoint is appended, the program will read the two-electron integrals from the files specified in $scfintunit, so there will be almost no loss of cpu-time.

All this information is normally provided by the previous dscf run if the keyword $scfdump (see there) was given.

$restartd data


Data provided by a previous dscf run that has been interrupted. This keyword is created when $scfdump was given.

$rundimensions data

is set by define so usually no changes are necessary. The dimensions must be greater or equal to those actually required, i.e. you can delete basis functions and keep rundimensions. This keyword is not necessary for small cases.
Example:

   dim(fock,dens)=6072
   natoms=6
   nshell=34
   nbf(CAO)=108
   nbf(AO)=98
   dim(trafo[SAO<-->AO/CAO])=256
   rhfshells=1

$scfconv integer


SCF convergency criterion will be 10-integer for the energy. Gradients will only be evaluated if integer > 6.

$scfdamp start=<.500> step=<.050> min=<.100>


Damping parameters for SCF iterations in order to reduce oscillations. The old Fock-operator is added to the current one with weight 0.5 as start; if convergence is good, this weight is then reduced by the step 0.05 in each successive iteration until the minimum of 0.1 is reached. (These are the default settings of define for closed-shell RHF). DSCF automatically tries to adjust the weight to optimize convergence but in difficult cases it is recommended to start with a large weight, e.g. 1.5, and to set the minimum to a larger value, e.g. 0.5.

$scfdebug options

Flags for debugging purposes. Following options are available:

vectors integer

Output level concerning molecular orbitals. integer=0 (default) means minimal output, >1 will output all start MOs and all MOs in each iteration.

density integer

Output level concerning difference density matrices.

debug integer

integer > 0 will dump a lot of information--be careful!

$scfdenapproxl integer


Direct SCF procedures build the Fock matrix by exploiting information from previous iterations for better efficiency. With this keyword information from the last integer iterations will be used. This feature is switched on with the default value 20, even if the keyword is absent. The user may reduce the number of iterations employed to smaller values (e.g. 10) in cases were numerical stability could become an issue. With the value 0 this feature is switched off; the Fock matrix is constructed from scratch in each iteration.

$scfdiis options

Control block for convergence acceleration via Pulay's DIIS .
Options are:

errvec=char

specifies the kind of error vector to be used (two different kind of DIIS algorithms)

char='FDS' or 'SDF' or 'FDS-SDF'

uses (FDS - SDF) as error vector.

char= none

no DIIS

char= sFDs

use S^-1/2FDS^1/2 - transposed

Further suboptions:

maxiter=integer

maximum number of iterations used for extrapolation.

debug=integer

debug level (default: 0)

integer=1

print applied DIIS coefficients

integer=2

print DIIS matrix and eigenvalues, too

qscal=real

scaling factor in DIIS procedure: qscal > 1 implies some damping, qscal = 1.0: straight DIIS.

thrd=real

directs the reduction of qscal to qscal = 1.0 (no damping in DIIS), done if || errvec|| < thrd.

Defaults for $prediag (see above) and $scfdiis

errvec=FDS-SDF, maxiter=5, qscal=1.2, thrd=0.0, this implies DIIS damping in all iterations, prediag is switched of.

Recommended:

errvec=sFDs leads to the following defaults:
qscal=1.2, for SCF runs: maxiter=6 and thrd=0.3, prediag is off; for DFT runs: maxiter=5 and thrd=0.1 prediag is on. If you want to switch off prediag put
$prediag none.

$scfdump


Dump SCF restart information onto data group $restartd and dump SCF MOs in each iteration onto $scfmo (scfdump = iter). Additionally, a data block $scfiterinfo will be dumped containing accumulated SCF total-, one- and two-electron energies of all previous SCF iterations. Information that will allow you to perform a restart if your calculation aborts will be dumped on data group $restartd (see also $restart).

$scfintunit options

Disc space specification for two-electron integrals. The following suboptions are available (and necessary):

unit=integer

Fortran unit number for this file. Unit numbers 30,31,... are recommended.

size=integer

Filespace in megabytes for this file. size=0 leads to a fully direct run. size is set by a statistics run, see $statistics. DSCF switches to direct mode if the file space is exhausted.

file=char

Filename. This may also be a complete path name, if you want to store the integrals in a special directory. Make sure the file is local, otherwise integrals are transmitted over the network.

Thus your data group $scfintunit may look like this:

$scfintunit          
 unit=30       size=35       file=twoint1
 unit=31       size=35       file=/users/work/twoint2

Maximal 30 files may be specified in this way.

$scfiterlimit integer


Maximum number of SCF iterations (default: 30).

$scfmo none file=char

Input/output data group for SCF MOs. You can specify

none

To perform a calculation without a start vector (i.e. use a core Hamiltonian guess).

file=char

The file where the MOs are written on output (default: mos).

These two options can also be used for $uhfmo_alpha and $uhfmo_beta to use a core guess and write the molecular orbitals to file.

After running define or a TURBOMOLE calculation additional options may appear specifying the origin of the MOs:

expanded

These MOs were obtained by projection form another basis set. They should not be used for wavefunction analysis.

scfconv=integer

The MOs are converged SCF MOs , the convergence criterion applied was 10^-integer

scfdump=integer

The MOs are unconverged SCF MOs which were written on this data group after iteration integer. The latter three options are mutually exclusive.

format(format string)

This specifies the FORTRAN format specification which was used for MO output. The standard format is (4d20.14). (See data group $mo output format.)

Example:
Your data group $scfmo could look like this after a successful TURBOMOLE run :

$scfmo  scfconv=7  format(3(1x,d19.13))
1  a1   eigenvalue=-.524127   nsao=6
.1234567890123d+01 -.1234567890123d+00  .1234567890123d-01 
.1234567890123d+01 -.1234567890123d+00 
3  a2   eigenvalue=-.234810  
...

$scforbitalorder on/off


Order SCF MOs with respect to their energies (default: on)

$scforbitalshift options

To assist convergence, either the energies of unoccupied MOs can be shifted to higher energies or, in open-shell cases, the energies of closed-shell MOs to lower energies. In general a large shift may help to get better convergence.

Options are:

noautomatic

Automatic virtual shell shift switched off.

automatic real

Automatic virtual shell shift switched on; the energies of virtual orbitals will be shifted if the HOMO-LUMO gap drops below real such that a gap of real is sustained. This is the default setting if the keyword is missing with real=0.1.

closedshell=real

Option for open-shell cases. Closed shells are shifted to lower energies by real. The default shift value is closedshell=0.4.
Note: Normally this will disable the automatic shift of energies of virtual orbitals! To override this, you should append an exclamation mark to the 'automatic' switch, i.e. specify 'automatic! real'.

individual

Set shifts for special occupied MOs. To use this option, start the line with the symmetry label and the list of MOs within this symmetry and append the desired shift in brackets as in the following example:

a1  1,2,4-6  (-.34)
b1  8        (+.3)

$scftol real


Integral evaluation threshold. Integrals smaller than real will not be evaluated. Note that this threshold may affect accuracy and the convergence properties if it is chosen too large. If $scftol is absent, a default value will be taken obtained from $scfconv by real = ${\frac{{10^{-(scfconv + 1)}}}{{3 \cdot \char93 bf}}}$ (#bf = number of basisfunctions).

$scratch files

The scratch files allocated by dscf can be placed anywhere in your file systems instead of the working directory by referencing their pathnames in this data group. All possible scratch files are listed in the following example:

$scratch files
    dscf    dens          path1/file1
    dscf    fock          path2/file2
    dscf    dfock         path3/file3
    dscf    ddens         path4/file4
    dscf    statistics    path7/file7
    dscf    errvec        path8/file8
    dscf    oldfock       path9/file9
    dscf    oneint        path10/file10

The first column specifies the program type (dscf stands for SCF energy calculations, i.e. the dscf program), the second column the scratch file needed by this program and the third column the pathname of the file to be used as scratch file.

$statistics options

The following options are allowed

off

Do not perform integrals statistics

dscf

Perform integrals statistics for dscf

kora

see KORA

mpgrad

see mpgrad

polly

see POLLY

dscf parallel

see PARALLEL PROCESSING

Options kora, dscf parallel, grad, mpgrad, polly will be described in the related chapters.
If $statistics dscf has been given integral prescreening will be performed (which is an n⁴-step and may therefore be time-consuming) and a table of the number of stored integrals as a function of the two parameters $thize and $thime will be dumped. Afterwards, the filespace needed for the current combination of $thize and $thime will be written to the data group ($scfintunit) and $statistics dscf will be replaced by $statistics off.

$thime integer


Integral storage parameter, which is related to the time needed to calculate the integral. The larger integer the less integrals will be stored. The default value is integer = 5. (see also $thize, $statistics)

$thize real


Integral storage parameter, that determines, together with $thime, the number of integrals stored on disc. Only integrals larger than real will be stored. The default value is real = 0.100E-04.