




Next: Restricted Open-Shell Hartree-Fock
Up: Hartree-Fock and DFT Calculations
Previous: Background Theory
Contents
Index
Exchange-Correlation Functionals Available
The following exchange-correlation functionals are available:
- LDAs: S-VWN, PWLDA
- GGAs: B-VWN, B-LYP, B-P, PBE
- MGGA: TPSS
- hybrid functionals: BH-LYP, B3-LYP, PBE0, TPSSh
- double-hybrid functional: B2-PLYP (energy calculations only!)
In detail, the functional library consists of:
- The Slater-Dirac exchange functional only (S)
[43,44].
- The 1980 correlation functional (functional V in the paper) of
Vosko, Wilk, and Nusair only (VWN) [45].
- A combination of the Slater-Dirac exchange and Vosko, Wilk,
and Nusair 1980 (functional V) correlation functionals (S-VWN)
[43,44,45].
- The S-VWN functional with VWN functional III in the paper. This
is the same functional form as available in the Gaussian program
[43,44,45].
- A combination of the Slater-Dirac exchange and Perdew-Wang
(1992) correlation functionals
[43,44,46].
- A combination of the Slater-Dirac exchange and Becke's 1988
exchange functionals (B88)
[43,44,47].
- Lee, Yang, and Parr's correlation functional (LYP)
[48].
- The B-LYP exchange-correlation functional (B88 exchange and LYP
correlation functionals)
[43,44,47,48].
- The B-VWN exchange-correlation functional (B88 exchange and VWN
(V) correlation functionals)
[43,44,47,45].
- The B-P86 exchange-correlation functional (B88 exchange, VWN(V)
and
Perdew's 1986 correlation functionals)
[43,44,47,45,49].
- The Perdew, Burke, and Ernzerhof (PBE) exchange-correlation
functional
[43,44,46,50].
- The Tao, Perdew, Staroverov, and Scuseria functional (Slater-Dirac, TPSS exchange and
Perdew-Wang (1992) and TPSS correlation functionals)
[43,44,46,51].
Additionally, for all four modules (dscf, grad, ridft, and rdgrad)
following hybrid
functionals are available (a mixture of Hartree-Fock exchange with DFT
exchange-correlation functionals):
- The BH-LYP exchange-correlation functional (Becke's
half-and-half exchange in a combination with the LYP correlation
functional) [43,44,47,48,52].
- The B3-LYP exchange-correlation functional (Becke's
three-parameter
functional) with the form,
| 0.8S + 0.72B88 + 0.2HF + 0.19VWN(V) + 0.81LYP |
(6.3) |
where HF denotes the Hartree-Fock exchange
[43,44,47,48,53].
- The B3-LYP exchange-correlation functional with VWN functional
V in the paper. This is the same functional form as available in the
Gaussian program.
- The 1996 hybrid functional of Perdew, Burke, and Ernzerhof,
with the form,
| 0.75(S + PBE(X)) + 0.25HF + PW + PBE(C) |
(6.4) |
where PBE(X) and PBE(C) are the Perdew-Burke-Ernzerhof
exchange and correlation functionals and PW is the Perdew-Wang
correlation functional
[43,44,46,50,54].
- The TPSSH exchange-correlation functional of Staroverov, Scuseria, Tao and Perdew with the
form,
| 0.9(S + TPSS(X)) + 0.1HF + PW + TPSS(C) |
(6.5) |
where HF denotes the Hartree-Fock exchange
[43,44,46,51,55].
- The Localized Hartree-Fock method (LHF) to obtain an effective
exact exchange Kohn-Sham potential [56,57] (module dscf only).
The LHF potential is:
vx(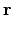 ) = ) = 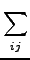 ns ns  - - 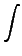 d d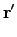 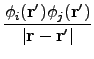 + 〈φi| vx - vxNL| φj〉 + 〈φi| vx - vxNL| φj〉 |
(6.6) |
where φ are Kohn-Sham occupied molecular orbitals, ns = 2 for closed-shell systems
and vxNL is the non-local Hartree-Fock operator.
Additionally the Double-Hydbrid Functional B2-PLYP can be used for single point
energy calculations. Note that one has to run an MP2 calculation after the DFT step to get the correct B2-PLYP energy!
B2-PLYP is a so-called double-hybrid density functional (DHDF)[58] that
uses in addition to a non-local exchange contribution (as in conventional hybrid-GGAs)
also a non-local perturbation correction for the correlation part. Note the
following options/restrictions in the present version of this method:
- single point calculations only (computed with the DSCF and RIMP2/RICC2 modules).
- UKS treatment for open-shell cases.
- can be combined with resolution-of-identity approximation for the SCF step (RI-JK option).
- can be combined with the dispersion correction (DFT-D method, s6(B2-PLYP)=0.55).
The non-local perturbation correction to the
correlation contribution is given by second-order
perturbation theory. The idea is rooted in the ab initio Kohn-Sham perturbation theory (KS-PT2) by
Görling and Levy[59,60]. The mixing is described by two empirical parameters
ax and ac in the following manner:
| EXC(DHDF) = (1 - ax)EX(GGA) + axEX(HF) |
|
|
(6.7) |
| + (1 - ac)EC(GGA) + acEC(KS - PT2), |
|
|
|
where EX(GGA) is the energy of a conventional exchange functional and EC(GGA) is the
energy of a correlation functional. EX(HF) is the Hartree-Fock exchange
of the occupied Kohn-Sham orbitals and
EC(KS - PT2) is a Møller-Plesset like
perturbation correction term based on the KS orbitals:
The method is self-consistent only with respect to
the first three terms in Eq. 6.7, i.e., first a SCF using a conventional hybrid-GGA is
performed first. Based on these orbitals
EC(KS - PT2) is evaluated
afterwards and added to the total energy.
For B2-PLYP, B88 exchange[47] and LYP correlation[48] are used with the
parameters ax = 0.53 and ac = 0.27. Due to the relatively large Fock-exchange fraction,
self-interaction error related problems are alleviated in B2-PLYP while unwanted side
effects of this (reduced account of static correlation) are damped or eliminated by the PT2 term.
1.2
How to use B2-PLYP:
- during preparation of your input with DEFINE select b2-plyp in the DFT menu.
- carry out a DSCF run. Prepare and run a RI-MP2 calculation with either RIMP2
or RICC2 program modules.
- the RI-MP2 program directly prints the B2PLYP energy if this functional has been chosen before
- if you use the RICC2 program the scaled (
ac = 0.27) second-order correlation energy.
must be added manually to the SCF-energy.
- in order to maintain consistency of the PT2 and GGA correlation parts, it is recommend
not to apply the frozen-core approximation in the PT2 treatment.





Next: Restricted Open-Shell Hartree-Fock
Up: Hartree-Fock and DFT Calculations
Previous: Background Theory
Contents
Index
TURBOMOLE

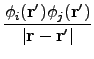 + 〈φi| vx - vxNL| φj〉
+ 〈φi| vx - vxNL| φj〉![$\displaystyle {\frac{{(ia\vert jb)[(ia\vert jb)-(ib\vert ja)]}}{{e_i+e_j-e_a-e_b}}}$](img54.png) .
.