




Next: Excited State Properties, Gradients
Up: First-Order Properties and Gradients
Previous: First-Order Properties and Gradients
Contents
Index
Ground State Properties, Gradients and Geometries
For CC2, one distinguishes between orbital-relaxed and unrelaxed properties.
Both are calculated as first derivatives of the respective energy
with respect to an external field corresponding to the calculated property. They
differ in the treatment of the SCF orbitals.
In the orbital-relaxed case the external field is (formally) already included
at the SCF stage and the orbitals are allowed to relax in the external field;
in the orbital-unrelaxed case the external field is first applied after the
SCF calculation and the orbitals do not respond to the external field.
Orbital-unrelaxed CC2 properties are calculated as first derivatives
of the real part of the unrelaxed Lagrangian [101]
Lur CC2(t,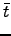 , β) , β) |
= |
〈HF| H| CC〉 +  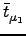 〈μ1| 〈μ1|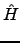 + [ + [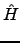 , T2]| HF〉 , T2]| HF〉 |
(9.12) |
| |
|
+ 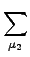 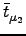 〈μ2| 〈μ2|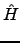 + [F0 + β + [F0 + β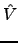 , T2]| HF〉 , T2]| HF〉 |
|
with
H = H0 + βV--where V is the (one-electron) operator
describing the external field, β the field strength, and H0 and
F0 are the Hamiltonian and Fock operators of the unperturbed system--by
the expression:
| 〈V〉ur CC2 |
= |
ℜ 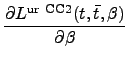 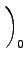 = = 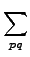 Durpq Vpq , Durpq Vpq , |
(9.13) |
| |
= |
ℜ 〈HF| 〈HF|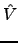 | HF〉 + | HF〉 +  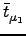 〈μ1| 〈μ1|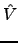 + [V, T2]| HF〉 + [V, T2]| HF〉 |
(9.14) |
| |
|
+ 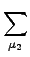 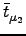 〈μ2|[ 〈μ2|[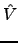 , T2]| HF〉 , T2]| HF〉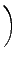 , , |
|
where ℜ indicates that the real part is taken.
Relaxed CC2 properties (and gradients) are calculated from the
the full variational density including the contributions from
the orbital response to the external perturbation, which are derived
from the Lagrangian [105,13]
Lrel CC2(t,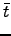 ) ) |
= |
〈HF| H| CC〉 +  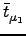 〈μ1| 〈μ1|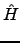 + [ + [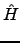 , T2]| HF〉 , T2]| HF〉 |
(9.15) |
| |
|
+ 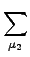 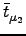 〈μ2| 〈μ2|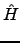 + [F, T2]| HF〉 + + [F, T2]| HF〉 + 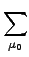 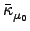 Fμ0 , Fμ0 , |
|
where F is the Fock operator corresponding to the Hamiltonian of the
perturbed system
H = H0 + βV.
One-electron properties are then obtained as:
| 〈V〉rel CC2 |
= |
ℜ 〈HF| 〈HF|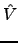 | HF〉 + | HF〉 +  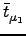 〈μ1| 〈μ1|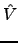 + [V, T2]| HF〉 + [V, T2]| HF〉 |
(9.16) |
| |
|
+ 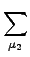 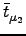 〈μ2|[V, T2]| HF〉 + 〈μ2|[V, T2]| HF〉 + 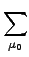 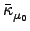 Vμ0 Vμ0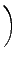 , , |
|
| |
= |
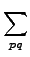 Drelpq Vpq . Drelpq Vpq . |
(9.17) |
The calculation of one-electron first-order properties requires that
in addition to the cluster equations also the linear equations for the
Lagrangian multipliers
 are solved, which requires similar
resources (CPU, disk space, and memory) as the calculation of a single
excitation energy.
For orbital-relaxed properties also a CPHF-like linear equation for the
Lagrangian multipliers
are solved, which requires similar
resources (CPU, disk space, and memory) as the calculation of a single
excitation energy.
For orbital-relaxed properties also a CPHF-like linear equation for the
Lagrangian multipliers
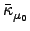 needs to be solved and
the two-electron density has to be build, since it is needed to set
up the inhomogeneity (right-hand side).
The calculation of relaxed properties is therefore somewhat more
expensive--the operation count for solving the so-called Z-vector
equations is similar to what is needed for an SCF calculation--and
requires also more disk space to keep intermediates for the
two-electron density--about
O(2V + 2N)Nx + Nx2 in addition to what
is needed for the solution of the cluster equations.
For ground states, orbital-relaxed first-order properties are
standard in the literature.
needs to be solved and
the two-electron density has to be build, since it is needed to set
up the inhomogeneity (right-hand side).
The calculation of relaxed properties is therefore somewhat more
expensive--the operation count for solving the so-called Z-vector
equations is similar to what is needed for an SCF calculation--and
requires also more disk space to keep intermediates for the
two-electron density--about
O(2V + 2N)Nx + Nx2 in addition to what
is needed for the solution of the cluster equations.
For ground states, orbital-relaxed first-order properties are
standard in the literature.
The calculation of the gradient implies the calculation of the same
variational densities as needed for relaxed one-electron properties
and the solution of the same equations. The construction of the
gradient contributions from the densities and derivative integrals
takes about the same CPU time as 3-4 SCF iterations and only
minor extra disk space.
For details of the implementation of CC2 relaxed first-order
properties and gradients and a discussion of applicability and
trends of CC2 ground-state equilibrium geometries
see ref. [13].
The following is in example input for a MP2 and CC2 single point
calculation of first-order properties and gradients:
$ricc2
mp2
cc2
$response
static relaxed operators=diplen,qudlen
gradient
A different input is required for geometry optimizations:
in this case the model for which the geometry should be optimized must be
specified in the data group $ricc2 by the keyword geoopt:
$ricc2
mp2
cc2
geoopt model=cc2
For CC2 calculations, the single-substitution part of
the Lagrangian multipliers
 are saved in the file
are saved in the file
CCL0--1--1---0 and can be kept for a restart (for MP2 and
CCS, the single-substitution part
 vanishes).
vanishes).
For MP2 only relaxed first-order properties and gradients are
implemented (unrelaxed MP2 properties are defined differently
than in CC response theory and are not implemented). For MP2,
only the CPHF-like Z-vector equations for
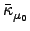 need to be solved, no equations have to be solved for
the Lagrangian multipliers
need to be solved, no equations have to be solved for
the Lagrangian multipliers
 .
CPU time and disk space requirements are thus somewhat smaller
than for CC2 properties or gradients.
.
CPU time and disk space requirements are thus somewhat smaller
than for CC2 properties or gradients.
For SCF/CIS/CCS it is recommended to use the modules
grad and rdgrad for the calculation of,
ground state gradients and first-order properties.





Next: Excited State Properties, Gradients
Up: First-Order Properties and Gradients
Previous: First-Order Properties and Gradients
Contents
Index
TURBOMOLE
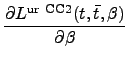
![]() are saved in the file
are saved in the file
![]() vanishes).
vanishes).
![]() need to be solved, no equations have to be solved for
the Lagrangian multipliers
need to be solved, no equations have to be solved for
the Lagrangian multipliers
![]() .
CPU time and disk space requirements are thus somewhat smaller
than for CC2 properties or gradients.
.
CPU time and disk space requirements are thus somewhat smaller
than for CC2 properties or gradients.