



Next: Disc space requirements:
Up: Characteristics of the Implementation
Previous: Perturbative triples corrections:
Contents
Index
The computationally most demanding (in terms floating point operations)
steps of a CCSD calculation are related to two kinds of terms.
One of the most costly steps is the contraction
ΩBaibj = 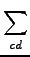 tcidj(ac| bd ) tcidj(ac| bd ) |
(10.16) |
where a, b, c, and d are virtual orbitals.
For small molecules with large basis sets or basis sets with diffuse
functions, where integral screening is not effective, it is time-determing
step and can most efficiently be evaluated with a minimal operation count of
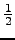 O2V2 (where O and V are number of, respectively
occupied and virtual orbitals), if the 4-index integrals (ac| bd ) in
the MO are precalculated and stored on file before the iterative solution
of the coupled-cluster equation, 10.4 and 10.5.
For larger systems, however, the storage and I/O of the integrals (ac| bd )
leads to bottlenecks. An alternatively, this contribution can be
evaluated in an integral-direct was as
O2V2 (where O and V are number of, respectively
occupied and virtual orbitals), if the 4-index integrals (ac| bd ) in
the MO are precalculated and stored on file before the iterative solution
of the coupled-cluster equation, 10.4 and 10.5.
For larger systems, however, the storage and I/O of the integrals (ac| bd )
leads to bottlenecks. An alternatively, this contribution can be
evaluated in an integral-direct was as
tκiλj = 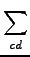 tci, djCκcCλd, ΩBμiνj = tci, djCκcCλd, ΩBμiνj = 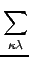 tκiλj(μκ| νλ), ΩBaibj = tκiλj(μκ| νλ), ΩBaibj = 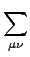 ΩBμiνjCμaCνb ΩBμiνjCμaCνb |
(10.17) |
which, depending on the implementation and system, has formally a
2-3 times larger operation count, but allows to avoid the storage
and I/O bottlenecks by processing the 4-index integrals on-the-fly
without storing them. Furthermore, integral screening techniques
can be applied to reduce the operation count for large systems to
asymptotic scaling with
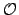 (
(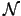 4).
4).
In TURBOMOLE only the latter algorithm is presently implemented.
(For small systems other codes will therefore be faster.)
The other class of expensive contributions are so-called ring terms
(in some publications denoted as C and D terms) which involve
contractions of the doubles amplitudes taibj with several
4-index MO integrals with two occupied and two virtual indeces,
partially evaluated with T1-dependent MO coefficients.
For these terms the implementation in TURBOMOLE employs the
resolution-of-the-identity (or density-fitting) approximation
(with the cbas auxiliary basis set) to reduce the overhead
from integral transformation steps.
Due this approximation CCSD energies obtained with TURBOMOLe
will deviate from those obtained with other coupled-cluster programs
by a small RI error. This error is usually in the same order or smaller
the RI error for a RI-MP2 calculation for the same system and basis sets.
The RI approximation is also used to evaluate the 4-index integrals
in the MO basis needed for the perturbative triples corrections.




Next: Disc space requirements:
Up: Characteristics of the Implementation
Previous: Perturbative triples corrections:
Contents
Index
TURBOMOLE