




Next: Advantages of the RI
Up: Second-Order Approximate Coupled-Cluster (CC2)
Previous: How to quote
Contents
Index
The CC2 ground-state energy
is--similarly to other coupled-cluster energies--obtained
from the expression
| ECC |
= 〈HF| H| CC〉 = 〈HF| H exp(T)| HF〉 , |
(9.1) |
| |
= ESCF + 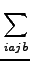 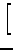 tabij + taitbj tabij + taitbj![$\displaystyle \Big]$](img137.png) 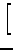 2(ia| jb) - (ja| ib) 2(ia| jb) - (ja| ib)![$\displaystyle \Big]$](img137.png) , , |
(9.2) |
where the cluster operator T is expanded as
T = T1 + T2 with
| T1 |
= 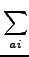 taiτai taiτai |
(9.3) |
| T2 |
= 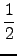 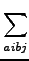 taibjτaibj taibjτaibj |
(9.4) |
(for a closed-shell case; in an open-shell case an additional spin
summation has to be included).
The cluster amplitudes tai and taibj are obtained as solution
of the CC2 cluster equations [101]:
| Ωμ1 |
= 〈μ1|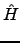 + [ + [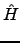 , T2]| HF〉 = 0 , , T2]| HF〉 = 0 , |
(9.5) |
| Ωμ2 |
= 〈μ2|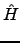 + [F, T2]| HF〉 = 0 , + [F, T2]| HF〉 = 0 , |
(9.6) |
with
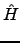
= exp(-
T1)
H exp(
T1),
where μ1 and μ2 denote, respectively, the sets
of all singly and doubly excited determinants.
The residual of the cluster equations
Ω(tai, taibj) is the
so-called vector function.
The recommended reference for the CC2 model is ref. [101],
the implementation with the resolution-of-the-identity approximation, RI-CC2,
was first described in ref. [10].
Subsections





Next: Advantages of the RI
Up: Second-Order Approximate Coupled-Cluster (CC2)
Previous: How to quote
Contents
Index
TURBOMOLE