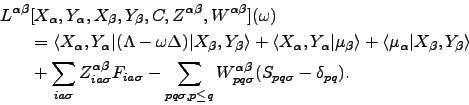Next: Implementation
Up: Hartree-Fock and DFT Response
Previous: Functionalities of Escf and
Contents
Index
We briefly state the basic working equations in the following, as far
as required to understand the program output. For a more detailed
treatment of the theory see refs.
[76,16,75,77,78]
and refs. therein.
The first-order frequency dependent response of the density matrix can
be expanded as
γ(x, x') = 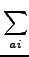 {Xai {Xai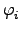 (x) (x)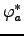 (x') + Yai (x') + Yai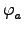 (x) (x)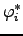 (x')}. (x')}. |
(7.1) |
The (real) expansion coefficients Xai and Yai are
conveniently gathered in a ``super-vector''
on L, the linear space of products of occupied and virtual ground
state MOs
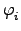 (x)
(x) (x') plus their complex
conjugates. X and Y describe the first-order change of the ground
state MOs due to an external perturbation which is represented by
(x') plus their complex
conjugates. X and Y describe the first-order change of the ground
state MOs due to an external perturbation which is represented by
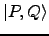 on L. For example, if an oscillating electric dipole
perturbation along the z axis is applied,
on L. For example, if an oscillating electric dipole
perturbation along the z axis is applied,
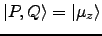 ,
where
,
where
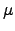 is the electric dipole operator.
is the electric dipole operator.
Next we define the 2×2 ``super-matrices''
where the four-index quantities A and B are the so-called ``orbital
rotation Hessians''. Explicit expressions for A and B can be
found, e.g., in ref. [16]. The vector
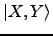 is
determined as the solution of the TDHF/TDDFT response problem,
is
determined as the solution of the TDHF/TDDFT response problem,
| (Λ - ωΔ)| X, Y〉 = - | P, Q〉. |
(7.4) |
If
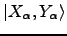 arises from an electric dipole
perturbation
arises from an electric dipole
perturbation
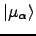 , the electronic dipole
polarizability at frequency ω is
, the electronic dipole
polarizability at frequency ω is
| ααβ(ω) = - 〈Xα, Yα| μβ〉, |
(7.5) |
α, β∈{x, y, z}. Similarly, if
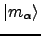 is a
component of the magnetic dipole moment operator, the optical rotation
is [79]
is a
component of the magnetic dipole moment operator, the optical rotation
is [79]
δαβ(ω) = - 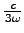 Im〈Xα, Yα| mβ〉, Im〈Xα, Yα| mβ〉, |
(7.6) |
where c is the light velocity.
Excitation energies Ωn are the poles of the
frequency-dependent density matrix response. They are thus the zeros
of the operator on the left-hand side of Eq. (7.4),
| (Λ - ΩnΔ)| Xn, Yn〉 = 0. |
(7.7) |
The corresponding eigenvectors
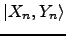 are the
transition density matrices for a given excitation (also called
``excitation vectors'' in the following). They are required to be
normalized according to
are the
transition density matrices for a given excitation (also called
``excitation vectors'' in the following). They are required to be
normalized according to
| 〈Xn, Yn| Δ| Xn, Yn〉 = 1. |
(7.8) |
Transition moments are evaluated by taking the trace with one-particle
operators, e.g.,
 0n = 〈Xn, Yn| 0n = 〈Xn, Yn| 〉 〉 |
(7.9) |
for the electric and
for the magnetic transition dipole moments.
The full TDHF/TDDFT formalism is gauge-invariant, i.e., the
dipole-length and dipole-velocity gauges lead to the same transition
dipole moments in the basis set limit. This can be used as a check for
basis set quality in excited state calculations. The TDA can formally
be derived as an approximation to full TDHF/TDDFT by constraining the
Y vectors to zero. For TDHF, the TDA is equivalent to configuration
interaction including all single excitations from the HF reference
(CIS). The TDA is not gauge invariant and does not
satisfy the usual sum rules [76], but it is somewhat less
affected by stability problems (see below).
Stability analysis of closed-shell electronic wavefunctions amounts to
computing the lowest eigenvalues of the electric
orbital rotation Hessian A + B, which decomposes into a singlet and a
triplet part, and of the magnetic orbital rotation Hessian
A - B. Note that A - B is diagonal for non-hybrid DFT, while A + B
generally is not. See refs. [80,15] for
further details.
Properties of excited states are defined as derivatives of the excited
state energy with respect to an external perturbation. It is
advantageous to consider a fully variational Lagrangian of the excited
state energy [16],
![\begin{displaymath}\begin{split}L[X,Y,\Omega,C,Z,W] & = E_{\text{GS}}+ \ensurema...
...} F_{ia} - \sum_{pq} W_{pq} (S_{pq} - \delta_{pq}). \end{split}\end{displaymath}](img130.png) |
(7.11) |
Here
EGS denotes the ground state energy, F and S are
the Fock and overlap matrices, respectively, and indices p, q run
over all, occupied and virtual MOs.
First, L is made stationary with respect to all its
parameters. The additional Lagrange multipliers Z and W enforce
that the MOs satisfy the ground state HF/KS equations and are
orthonormal. Z is the so-called Z-vector, while W turns out to
be the excited state energy-weighted density matrix. Computation of
Z and W requires the solution of a single static TDHF/TDKS
response equation (7.4), also called coupled and perturbed HF/KS
equation. Once the relaxed densities have been computed, excited state
properties are obtained by simple contraction with derivative
integrals in the atomic orbital (AO) basis. Thus, computation of
excited state gradients is more expensive than that of ground state
gradients only by a constant factor which is usually in the range of
1…4.
TDHF/TDDFT expressions for components of the frequency-dependent
polarizability
ααβ(ω) can also be reformulated
as variational polarizability Lagrangians [81]
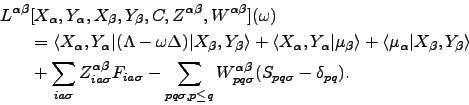 |
(7.12) |
The stationary point of
Lαβ(ω) equals to
- ααβ(ω). The requirement that
Lαβ(ω) be stationary with respect to all variational
parameters determines the Lagrange multipliers
Zαβ and
Wαβ. All polarizability components
αβ are
processed simultaneously which allows for computation of polarizability
derivatives at the computational cost which is only 2-3 higher than for
the electronic polarizability itself.





Next: Implementation
Up: Hartree-Fock and DFT Response
Previous: Functionalities of Escf and
Contents
Index
TURBOMOLE


![]() arises from an electric dipole
perturbation
arises from an electric dipole
perturbation
![]() , the electronic dipole
polarizability at frequency ω is
, the electronic dipole
polarizability at frequency ω is
![\begin{displaymath}\begin{split}L[X,Y,\Omega,C,Z,W] & = E_{\text{GS}}+ \ensurema...
...} F_{ia} - \sum_{pq} W_{pq} (S_{pq} - \delta_{pq}). \end{split}\end{displaymath}](img130.png)