




Next: Hartree-Fock and DFT Response
Up: Hartree-Fock and DFT Calculations
Previous: Calculation Setup
Contents
Index
Empirical Dispersion Correction for DFT Calculations
Based on an idea that has earlier been proposed for Hartree-Fock calculations[70,71],
an general empirical dispersion correction has been proposed by Stefan Grimme for density functional
calculations [72]. A modified version of the approach with extension
to more elements and more functionals has been published in ref. [73].
The correction is invoked by the keyword $disp in the control file. The parameters
of the second DFT-D publication are used. The older parameters are used when the
keyword $olddisp is found in the control file.
When using the dispersion correction, the total energy is given by
| EDFT-D = EKS-DFT + Edisp |
(6.9) |
where
EKS-DFT is the usual self-consistent Kohn-Sham energy as obtained from the chosen
functional and Edisp is an empirical dispersion correction given by
Edisp = - s6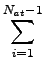 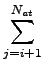  fdmp(Rij) . fdmp(Rij) . |
(6.10) |
Here, Nat is the number of atoms in the system, C6ij denotes the dispersion coefficient
for atom pair ij, s6 is a global scaling factor that only
depends on the DF used and Rij is an interatomic distance.
The interatomic C6ij term is calculated as geometric mean of the form
C6ij =  . . |
(6.11) |
This yields much better results that the form used in the original paper:
C6ij = 2⋅ |
(6.12) |
In order to avoid near-singularities for small R, a damping function fdmp
must be used which is given by
fdmp(Rij) = 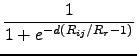 |
(6.13) |
where Rr is the sum of atomic vdW radii. These values are derived from
the radius of the 0.01 a0-3 electron density contour from ROHF/TZV computations of the atoms
in the ground state. An earlier[72] used general scaling factor for the radii is decreased
from 1.22 to 1.10 in the second implementation. This improves computed intermolecular distances
especially for systems with heavier atoms. The atomic van der Waals radii R0
used are given in Table 6.3 together with new atomic C6 coefficients (see below).
Compared to the original parameterization (d = 23), a smaller damping parameter of d = 20 provides
larger corrections at intermediate distances (but still negligible dispersion energies for
typical covalent bonding situations).
Table 6.2:
s6 parameters for functionals in the old and the revised implementation of DFT-D
|
Density Functional | s6 | s6 (old) |
| BP86 | 1.05 | 1.30 |
|
B-LYP | 1.20 | 1.40 |
|
PBE | 0.75 | 0.70 |
|
B3-LYP | 1.05 | -a |
|
TPSS | 1.00 | -a |
a Not available
b See Ref.[74]
|
Table 6.3:
C6 parametersa (in
Jnm6mol-1)
and van der Waals radiib R0 (in Å) for elements H-Xe.
|
element | C6 | R0 | element | C6 | R0 |
| H | 0.14 | 1.001 | K | 10.80c | 1.485 |
|
He | 0.08 | 1.012 | Ca | 10.80c | 1.474 |
|
Li | 1.61 | 0.825 | Sc-Zn | 10.80c | 1.562d |
|
Be | 1.61 | 1.408 | Ga | 16.99 | 1.650 |
|
B | 3.13 | 1.485 | Ge | 17.10 | 1.727 |
|
C | 1.75 | 1.452 | As | 16.37 | 1.760 |
|
N | 1.23 | 1.397 | Se | 12.64 | 1.771 |
|
O | 0.70 | 1.342 | Br | 12.47 | 1.749 |
|
F | 0.75 | 1.287 | Kr | 12.01 | 1.727 |
|
Ne | 0.63 | 1.243 | Rb | 24.67c | 1.628 |
|
Na | 5.71c | 1.144 | Sr | 24.67c | 1.606 |
|
Mg | 5.71c | 1.364 | Y-Cd | 24.67c | 1.639d |
|
Al | 10.79 | 1.639 | In | 37.32 | 1.672 |
|
Si | 9.23 | 1.716 | Sn | 38.71 | 1.804 |
|
P | 7.84 | 1.705 | Sb | 38.44 | 1.881 |
|
S | 5.57 | 1.683 | Te | 31.74 | 1.892 |
|
Cl | 5.07 | 1.639 | I | 31.50 | 1.892 |
|
Ar | 4.61 | 1.595 | Xe | 29.99 | 1.881 |
a Derived from UDFT-PBE0/QZVP computations.
b Derived from atomic ROHF/TZV computations.
c Average of preceeding group VIII and following group III element.
d Average of preceeding group II and following group III element.
|
Table 6.4:
old C6 parametersa (in
Jnm6mol-1)
and van der Waals radiib R0 (in Å) for elements H-Ne.
|
element | C6 | R0 | element | C6 | R0 |
| H | 0.16 | 1.11 | O | 0.70 | 1.49 |
|
C | 1.65 | 1.61 | F | 0.57 | 1.43 |
|
N | 1.11 | 1.55 | Ne | 0.45 | 1.38 |
a Derived from UDFT-PBE0/QZVP computations.
b Derived from atomic ROHF/TZV computations.
|
Caution: if elements are present in the molecule for which no parameters are
defined, the calculation proceeds with an atomic C6 parameter of 0.0.
This results in an incomplete description of the dispersion energy.





Next: Hartree-Fock and DFT Response
Up: Hartree-Fock and DFT Calculations
Previous: Calculation Setup
Contents
Index
TURBOMOLE
 .
.