



Next: Calculation Setup
Up: Periodic Electrostatic Embedded Cluster
Previous: General Information
Contents
Index
Generally, the PEEC method divides the entire, periodic and infinite
system into two parts, the inner (I) part, or so called cluster, and
the outer (O) part which describes its environment. Thus, unlike "true"
periodic quantum mechanical methods, PEECM primarily aims at
calculations of structure and properties of localized defects in
dominantly ionic crystals. The innermost part of the cluster is
treated quantum mechanically (QM), whereas in the remaining cluster
part cations are replaced by effective core potentials (ECPs) and
anions by ECPs or by simply point charges. Such an "isolating" outer
ECP shell surrounding the actual QM part is necessary in order to
prevent artificial polarization of the electron density by cations
which would otherwise be in a direct contact with the QM boundary.
The outer part or the environment of the cluster is described by a
periodic array of point charges, representing cationic and anionic
sites of a perfect ionic crystal.
The electronic Coulomb energy term arising from the periodic field of point
charges surrounding the cluster has the following form
where UC denotes the unit cell of point charges,
Dμν are
elements of the density matrix, μ, ν are basis functions,
qk, 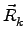 denote charges and positions of point charges, and
denote charges and positions of point charges, and
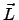 denote direct lattice vectors of the outer part O. It is evaluated using the
periodic fast multipole method (PFMM) [68] which, unlike
the Ewald method [69], defines the lattice sums entirely
in the direct space. In general, PFMM yields a different electrostatic
potential then the Ewald method, but the difference is merely a
constant shift which depends on the shape of external infinite surface
of the solid (i.e. on the way in which the lattice sum converges toward
the infinite limit). However, this constant does not influence
relative energies which are the same as obtained using the Ewald
method, provided that the total charge of the cluster remains
constant. Additionally, since the electrostatic potential within a
solid is not a well defined quantity, both the absolute total energies
and orbital energies have no meaning (i.e. you cannot compare energies
of neutral and charged clusters!).
denote direct lattice vectors of the outer part O. It is evaluated using the
periodic fast multipole method (PFMM) [68] which, unlike
the Ewald method [69], defines the lattice sums entirely
in the direct space. In general, PFMM yields a different electrostatic
potential then the Ewald method, but the difference is merely a
constant shift which depends on the shape of external infinite surface
of the solid (i.e. on the way in which the lattice sum converges toward
the infinite limit). However, this constant does not influence
relative energies which are the same as obtained using the Ewald
method, provided that the total charge of the cluster remains
constant. Additionally, since the electrostatic potential within a
solid is not a well defined quantity, both the absolute total energies
and orbital energies have no meaning (i.e. you cannot compare energies
of neutral and charged clusters!).




Next: Calculation Setup
Up: Periodic Electrostatic Embedded Cluster
Previous: General Information
Contents
Index
TURBOMOLE
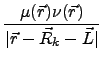 d
d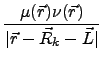 d
d