




Next: How to use
Up: Two-component Hartree-Fock and DFT
Previous: Two-component Hartree-Fock and DFT
Contents
Index
Two-component treatments allow for self-consistent calculations including
spin-orbit interactions. These may be particularly important for compounds
containing heavy elements (additionally to scalar relativistic
effects). Two-component treatments were implemented within the module ridft for
RI-JK-Hartree-Fock and RI-DFT (local, gradient-corrected and hybrid functionals)
via effective core potentials describing both scalar and spin-orbit relativistic
effects.
The theoretical background and the implementation is described
in [61].
Two-component treatments require the use of complex two-component orbitals
ψi( ) = ) =  |
|
instead of real (non-complex) one-component orbitals needed for
non-relativistic or scalar-relativistic treatments.
The Hartree-Fock and Kohn-Sham equations are now spinor equations
with a complex Fock operator
The wavefunction is no longer eigenfunction of the spin operator,
the spin vector is no longer an observable.
In case of DFT for open-shell systems rotational invariance of the exchange-correlation
energy was ensured by the non-collinear approach. In this approach the exchange-correlation
energy is a functional of the particle density and the absolute value of the spin-vector density
 (
(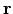 ) (
) (
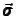 are the Pauli matrices)
are the Pauli matrices)
This quantity replaces the spin-density (difference between density of alpha and beta electrons) of
non- or scalar-relativistic treatments.
For closed-shell species the Kramers-restricted scheme, a generalization of the RHF-scheme of one
component treatments, is applicable.





Next: How to use
Up: Two-component Hartree-Fock and DFT
Previous: Two-component Hartree-Fock and DFT
Contents
Index
TURBOMOLE


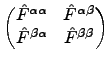
 = εi
= εi .
.![]() (
(![]() ) (
) (
![]() are the Pauli matrices)
are the Pauli matrices)