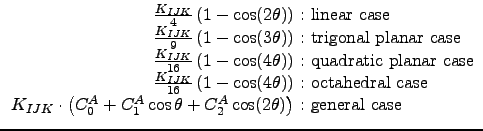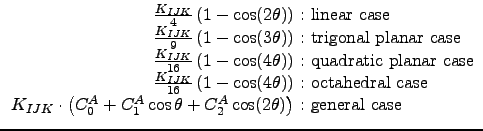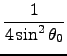



Next: Molecular Dynamics Calculations
Up: Force Field Calculations
Previous: How to Perform a
Contents
Index
The uff implementation follows the paper by Rappé [7].
The energy expression in uff is as follows:
| E UFF = |
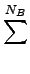 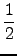 ⋅KIJ⋅ ⋅KIJ⋅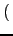 r - rIJ r - rIJ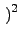 |
(5.1) |
| + |
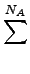  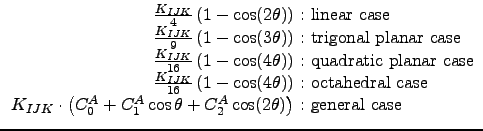 |
|
| + |
 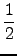 ⋅Vφ⋅ ⋅Vφ⋅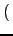 1 - cos 1 - cos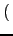 nφ0 nφ0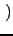 cos(nφ) cos(nφ)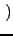 |
|
| + |
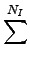 Vω⋅ Vω⋅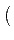 CI0 + CI1cosω + CI2cos 2ω CI0 + CI1cosω + CI2cos 2ω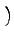 |
|
| + |
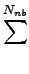 DIJ⋅ DIJ⋅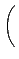 -2 -2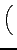 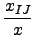 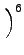 + + 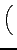 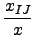 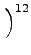 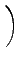 |
|
| + |
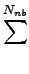 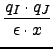 |
|
The Fourier coefficients
CA0, CA1, CA2 of the general angle terms
are evaluated as a function of the natural angle θ0:
| CA2 |
= 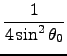 |
(5.2) |
| CA1 |
= - 4⋅CA2cosθ0 |
(5.3) |
| CA0 |
= CA2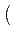 2 cos2θ0 + 1 2 cos2θ0 + 1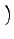 |
(5.4) |
The expressions in the engery term are:
-
NB, NA, NT, NI, Nnb
- the numbers of the bond-,
angle-, torsion-, inversion- and the non bonded-terms.
-
KIJ, KIJK
- forceconstants of the bond- and
angle-terms.
- r, rIJ
- bond distance and natural bond
distance of the two atoms I and J.
-
θ, θ0
- angle and natural angle for
three atoms I - J - K.
-
CA0, CA1, CA2
- Fourier coefficients of the general
angle terms.
-
φ, φ0
- torsion angle and natural torison
angle of the atoms I - J - K - L.
- Vφ
- height of the torsion barrier.
- n
- periodicity of the torsion potential.
- ω
- inversion- or out-of-plane-angle at atom I.
- Vω
- height of the inversion barrier.
-
CI0, CI1, CI2
- Fourier coefficients of the
inversions terms.
- x, xIJ
- distance and natural distance of two
non bonded atoms I and J.
- DIJ
- depth of the Lennard-Jones potential.
-
qI, ε
- partial charge of atoms I and dielectric
constant.
One major difference in this implementation concerns the atom types.
The atom types in Rappé's paper have an underscore "_". In the
present implementation an sp3 C atom has the name "C 3" instead of
"C_3". Particularly the bond terms are described with the harmonic
potential and the non-bonded van der Waals terms with the
Lennard-Jones potential. The partial charges needed for electrostatic
nonbond terms are calculated with the Charge Equilibration Modell
(QEq) from Rappé [34]. There is no cutoff for the
non-bonded terms.
The relaxation procedure distinguishes between molecules wih more than
90 atoms and molecules with less atoms. For small molecules it
consists of a Newton step followed by a linesearch step. For
big molecules a quasi-Newton relaxation is done. The BFGS
update of the force-constant matric is done [35,36,29,37]. Pulay's DIIS
procedure is implemented for big molecule to accelarate the
optimization [38,28].
The coordinates for any single atom can be fixed by placing an 'f'
in the third to eighth column of the chemical symbol/flag group.
As an example, the following coordinates specify acetone with a fixed
carbonyl group:
$coord
2.02693271108611 2.03672551266230 0.00000000000000 c
1.08247228252865 -0.68857387733323 0.00000000000000 c f
2.53154870318830 -2.48171472134488 0.00000000000000 o f
-1.78063790034738 -1.04586399389434 0.00000000000000 c
-2.64348282517094 -0.13141435997713 1.68855816889786 h
-2.23779643042546 -3.09026673535431 0.00000000000000 h
-2.64348282517094 -0.13141435997713 -1.68855816889786 h
1.31008893646566 3.07002878668872 1.68840815751978 h
1.31008893646566 3.07002878668872 -1.68840815751978 h
4.12184425921830 2.06288409251899 0.00000000000000 h
$end




Next: Molecular Dynamics Calculations
Up: Force Field Calculations
Previous: How to Perform a
Contents
Index
TURBOMOLE