



Next: Definition of Internal Coordinates
Up: Program Relax
Previous: Optimization of General Coordinates
Contents
Index
In a Newton-type geometry update procedure often only a crude
approximation to the force constant matrix Hk is available. What
can be done then is to update
Fk = (Hk)-1 in each iteration using
information about previous coordinates and gradients. This constitutes
the quasi-Newton or variable metric methods of which there are a few
variants:
- Murtagh/Sargent (MS):
Fk = Fk-1 + 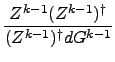 |
|
- Broyden/Fletcher/Goldfarb/Shanno (BFGS):
Fk = Fk-1 + 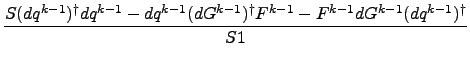 |
|
- Davidon/Fletcher/Powell (DFP):
Fk = Fk-1 + 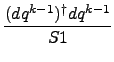 - - 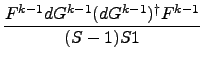 |
|
- combined method (BFGS/DFP): If
S1 < (S - 1)S1 and S1 > 0
perform DFP update, otherwise BFGS.
The meaning of the symbols above is as follows:
-
Fk = (Hk)-1
- approximate inverse force constant
matrix in the k-th iteration.s
- qk
- general coordinates in the k-th iteration.
- Gk
- gradients in the k-th iteration.
-
dqk-1 = qk - qk-1
-
dgk-1 = gk - gk-1
-
Zk-1 = dqk-1 - Fk-1dGk-1
-
S1 = (dqk-1)†dgk-1
-
S = 1 + ((dgk-1)†Fk-1dGk-1)/(S1)
-
An alternative is to use update algorithms for the hessian Hk
itself:
Ehrig, Ahlrichs :
Diagonal update for the hessian by means of a least squares fit
Hkii = 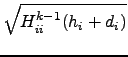 |
|
with the new estimate h for the diagonal elements obtained by
hi = 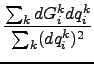 |
|
and the error d obtained by the regression
di = 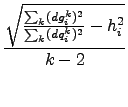 . . |
|
Another alternative is to use DIIS-like methods: structure
optimization by direct inversion in the iterative subspace. (See ref.
[28] for the description of the algorithm). The DIIS
procedure can often be applied with good success, using static or
updated force constant matrices.
Any of the algorithms mentioned above may be chosen. Recommended is
the macro option ahlrichs, which leads to the following actions
(n is the maximum number of structures to be included for the
update, default is n = 4):
-
ncycles < n:
- geometry update by
inter/extrapolation using the last 2 geometries.
-
ncycles≥n:
- diagonal update for the
hessian as described above; DIIS-like update for the geometry.
-
|| G|| < thr:
- BFGS-type update of the
hessian and quasi-Newton update of (generalized) coordinates.
References for the algorithms mentioned above:
[29,25,30,28,31,32]




Next: Definition of Internal Coordinates
Up: Program Relax
Previous: Optimization of General Coordinates
Contents
Index
TURBOMOLE
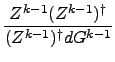
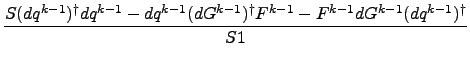
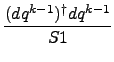 -
- 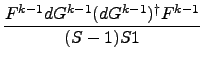
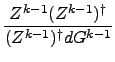
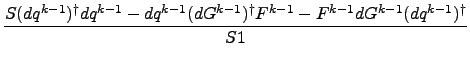
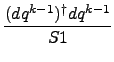 -
- 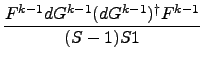
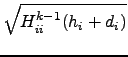
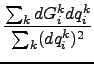
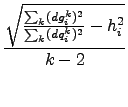 .
.